论文 arXiv 页面截图

论文 arXiv 页面截图
大型语言模型(LLMs)在各种任务中展现了令人印象深刻的能力,然而,它们执行结构化符号规划的能力仍然有限,特别是在需要像规划领域定义语言(PDDL)这样的形式化表示的领域。在本文中,我们提出了一种新颖的指令调优框架,PDDL-INSTRUCT,旨在通过逻辑思维链推理来增强LLMs的符号规划能力。我们的方法侧重于教导模型使用显式的逻辑推理步骤,严格地对动作的适用性、状态转换和规划的有效性进行推理。通过开发指导模型精确进行逻辑推理的指令提示,以确定在给定状态下何时可以应用动作,我们使LLMs能够通过结构化反思来自我纠正其规划过程。该框架通过将规划过程分解为关于前置条件满足、效果应用和不变量保持的显式推理链,系统地构建验证技能。在多个规划领域的实验结果表明,我们基于思维链推理的指令调优模型在规划方面表现明显更好,在标准基准测试中实现了高达94%的规划准确率,比基线模型提高了66%的绝对值。这项工作弥合了LLMs的一般推理能力与自动化规划所需的逻辑精度之间的差距,为开发更好的人工智能规划系统提供了一个有前景的方向。
像GPT [OpenAI et al., 2023]、Gemini [Team et al., 2023]、LLAMA [Touvron et al., 2023]等大型语言模型(LLMs)在包括数学和编码在内的各个领域都取得了显著的成功 [Imani et al., 2023, Gaur and Saunshi, 2023, Romera-Paredes et al., 2023, Ahn et al., 2024]。然而,它们在执行结构化符号规划方面的能力仍然存在一个关键的差距,这是可靠的现实世界序贯决策系统所需的基本能力。最近的研究强调了这个问题,即虽然LLMs擅长对非结构化文本进行一般推理,但它们在自动化规划任务所需的逻辑推理和系统验证方面存在困难 [Stechly et al., 2023, Valmeekam et al., 2023a,c, Kambhampati et al., 2024, Stechly et al., 2025]。
当考虑像规划领域定义语言(PDDL)[McDermott et al., 1998]这样的形式化规划表示时,这一局限性变得尤为明显。尽管在特定配置下取得了一些有希望的结果[Liu et al., 2023, Wang et al., 2024],但这些模型在包括经典规划在内的多步推理任务上通常表现不佳[Hsiao et al., 2025]。这对规划任务有重大影响,因为规划任务是PSPACE完备的[Bylander, 1991],并且本质上需要随着问题复杂性的增加而扩展推理努力。
在本文中,我们通过引入PDDL-INSTRUCT来挑战这一局限性,这是一个新颖的框架(如图1所示),它用自动化规划所需的形式化推理来增强LLMs的推理能力。PDDL-INSTRUCT明确地教导LLMs使用逻辑思维链提示来推理规划领域的前置条件-效果结构。通过将规划验证分解为原子推理步骤,并将此结构纳入指令调优,我们的方法使LLMs不仅能生成语法正确的规划,还能通过分步推理来验证其逻辑有效性。这种执行结构化验证的能力显著增强了LLM生成规划的可靠性,并为通过迭代细化进行自我纠正开辟了可能性。
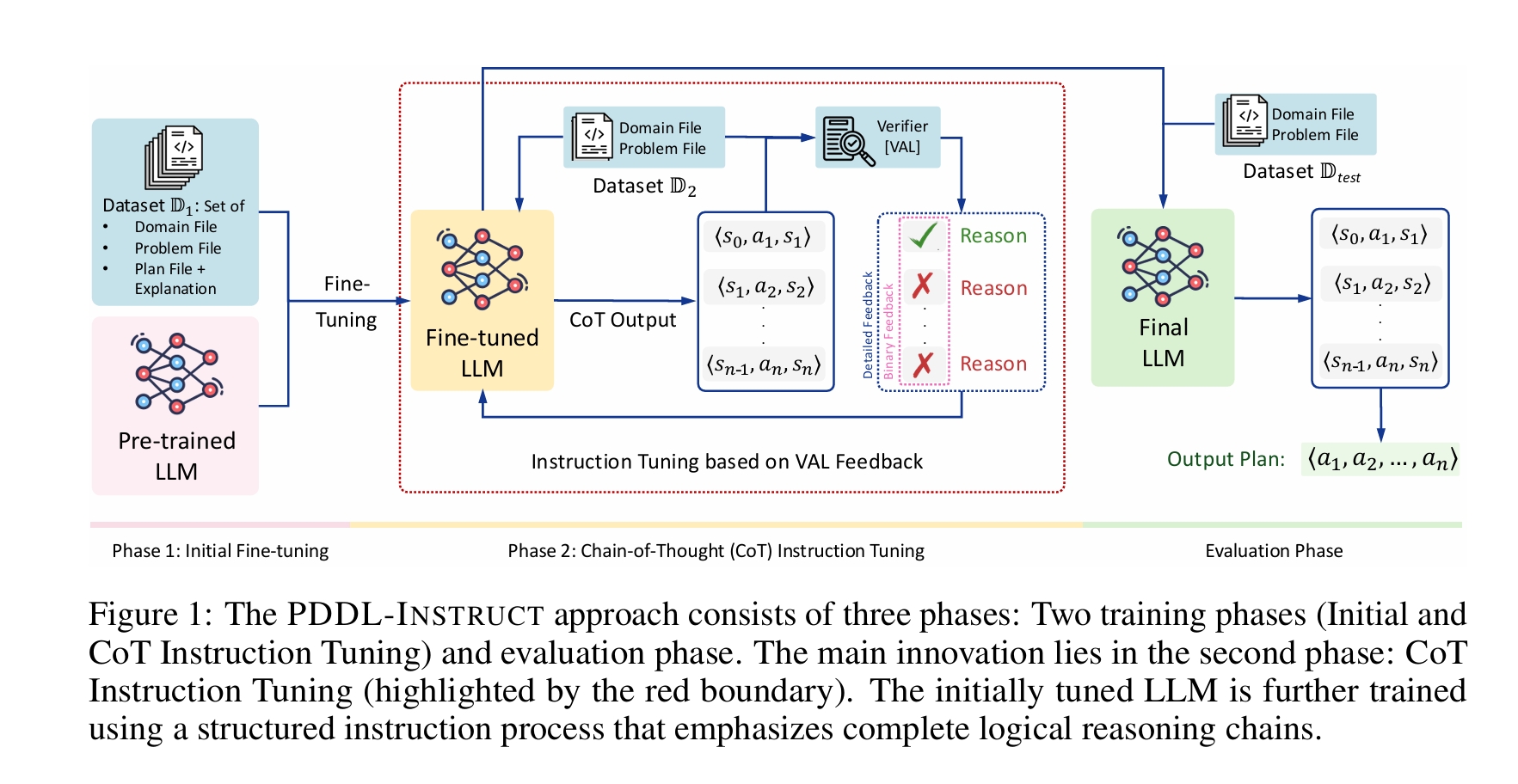
[图1:PDDL-INSTRUCT方法包括三个阶段:两个训练阶段(初始和CoT指令调优)和评估阶段。主要创新在于第二阶段:CoT指令调优(由红色边界突出显示)。初始调优的LLM使用强调完整逻辑推理链的结构化指令过程进行进一步训练。]
本文的主要贡献是:
我们的结果表明,PDDL-INSTRUCT显著优于基线模型和传统指令调优模型,在标准规划领域中实现了高达94%的规划有效率。这项工作不仅解决了当前LLM能力的一个关键局限,也为开发能够在复杂场景中进行可靠规划的更值得信赖的人工智能系统提供了基础。
用于规划的LLMs 最近有多种方法被用于规划,例如生成可执行代码来规定规划行为[Liang et al., 2023, Singh et al., 2023, Nijkamp et al., 2023, Wang et al., 2025],使用带环境反馈的闭环[Huang et al., 2022, Song et al., 2023]或用于自我完善[Wang et al., 2023, Zhou et al., 2024]。一些最近的方法还使用LLMs为规划合成Python程序[Silver et al., 2024, Hao et al., 2025b, Chen et al., 2025b, Corrêa et al., 2025]。
然而,正如[Tantakoun et al., 2025]所总结的,LLMs在长期规划和推理方面面临挑战,经常产生不可靠的规划[Stechly et al., 2024, Pallagani et al., 2023, Momennejad et al., 2023],随着规模的扩大,它们常常无法考虑到动作的效果和要求[Stechly et al., 2024],并且其性能会随着自我迭代反馈而下降[Stechly et al., 2023, Valmeekam et al., 2023a, Huang et al., 2025]。
另一种方法是使用LLMs生成自动化规划模型(例如PDDL领域和问题),并依赖现有的符号求解器来产生可靠的解决方案。这种混合范式引起了广泛关注[Huang et al., 2025, Mahdavi et al., 2024, Zhang et al., 2025b, Tantakoun et al., 2025]。然而,准确生成这样的结构化模型对LLMs来说是具有挑战性的。为了达到高准确性,该过程通常依赖于人类干预以获取反馈和验证[Guan et al., 2023],使用外部验证器[Silver et al., 2024, Hao et al., 2025a],或专注于问题的有限方面(例如仅生成规划目标[Xie et al., 2023])。NL2P [Gestrin et al., 2024]提出使用显式推理步骤和思维链反向提示从自然语言输入中生成PDDL领域和问题。在这里,我们建议微调一个LLM来学习显式推理步骤,以推理动作适用性、状态转换和规划有效性,从而生成一个规划。
用于规划的微调显著提高了模型生成符号规划的能力[Pallagani et al., 2023, Li et al., 2025, Fu et al., 2025]。然而,这种方法的主要缺点是其高昂的经济、时间和计算成本,以及模型的可转移性下降。微调使模型专门化于训练过的领域和问题类型,对新问题的可转移性较差。
指令调优 已成为NLP中一种重要的方法,以实现在未见任务上的零样本泛化[Mishra et al., 2022, Wei et al., 2022a, Ouyang et al., 2022]。这种技术涉及微调大型语言模型,通过遵循指令来执行各种任务,使得任务来源对于有效的调优至关重要[Longpre et al., 2023]。虽然现有方法通常依赖于来自数据集(如TO [Sanh et al., 2022]、FLAN [Wei et al., 2022a, Longpre et al., 2023]和NaturalInstructions [Mishra et al., 2022, Wang et al., 2022])的人工众包任务,但这些高质量资源需要大量的人力,并且数量通常有限。另一种方法是模型生成的任务,其中强大的语言模型(如GPT-3和GPT-4)生成多样的指令和任务对[Wang et al., 2022, Peng et al., 2023],尽管当输出与输入不正确对应时,这可能会引入噪音。在这项工作中,我们通过利用自动化规划任务生成器[Seipp et al., 2022, Valmeekam et al., 2023b]来创建指令调优数据集,从而缓解了这个问题。
思维链推理 提高LLM推理能力的一个重要进展是思维链(CoT)提示的实现[Wei et al., 2022b]。通过生成显式的中间推理步骤,这些模型现在可以解决复杂的逻辑推导和多步问题解决。短CoT方法[Lambert et al., 2025, Kojima et al., 2022]在简单问题上显示出有效性,但在面对更复杂的挑战时暴露了局限性。向更长推理链的演变随后改变了机器推理的格局。Stechly et al. [2024]认为,尽管CoT对推理任务有效,但不适用于规划,但在这项工作中,我们表明,通过使用更好的提示与指令调优进行适当整合,CoT确实可以用于规划任务。
自动化规划 在本节中,我们简要描述自动化规划。更多细节请参考 Geffner and Bonet [2013] 和 Chen et al. [2025a]。
一个自动化规划问题可以被形式化地描述为一个元组 $\langle P, A, s_0, G \rangle$,其中 $P$ 是一组用于描述离散且完全可观察状态 $S$ 的流(fluents),$A$ 代表一个有限的动作集合,$s_0 \in S$ 表示初始状态,$G$ 指定了目标条件。每个动作 $a_i \in A$ 被定义为 $\langle pre(a_i), add(a_i), del(a_i) \rangle$,其中 $pre(a_i)$ 是为了使动作可执行,当前状态必须满足的流的集合,$add(a_i)$ 是执行后变为真的流的集合,$del(a_i)$ 是执行后变为假的流的集合。注意,经典规划中的状态空间 $S$ 来自于对流集合所有可能的真值分配。
一个规划问题 $P$ 的解决方案,称为一个规划 $\pi$,是一个动作序列 $\langle a_0, a_1, ..., a_{n-1} \rangle$,它在 $n$ 步后将初始状态转换为满足目标条件的状态。注意 $\pi$ 产生状态转换 $s_{i+1} = a_i(s_i) = (s_i \setminus del(a_i)) \cup add(a_i)$ 对于所有 $0 \le i < n$ 使得 $s_n \in G$。如果一个规划 $\pi$ 使用最少的动作数(在本文中,我们考虑动作成本统一)达到目标状态,则被认为是最优的;而如果它成功达到目标但使用的动作数多于最优规划,则被认为是满足的(satisficing)。
规划领域定义语言(PDDL)[McDermott et al., 1998],基于STRIPS [Fikes and Nilsson, 1971],为自动化规划问题提供了一个标准化的规范。PDDL由一个领域 $\mathcal{D} = \langle P, A \rangle$ 和一个问题 $\mathcal{P} = \langle s_0, G \rangle$ 组成,领域包含流 $P$ 和动作 $A$ 的集合(以及它们的前置条件、增加和删除集),问题包含初始状态 $s_0$ 和目标条件 $G$。
指令调优 [Mishra et al., 2022, Wei et al., 2022a, Ouyang et al., 2022] 是一种在标记数据集上微调LLMs的方法。考虑一个指令调优数据集 $\mathbb{D}_1 = \{(x_i, r_i)\}_{i=1}^N$ 包含标记样本,其中 $x_i$ 代表一个指令,$r_i$ 是其对应的理想响应。我们将我们的大型语言模型表示为 $\mathcal{M}_\theta$,参数为 $\theta$。模型为给定的指令 $x_i$ 产生输出 $y_i = \mathcal{M}_\theta(x_i)$。标准的指令调优目标是找到模型参数 $\theta^*$,以最小化模型预测 $(\mathcal{M}_\theta(x))$ 和目标响应 $(r)$ 在整个指令数据集(数据集 $\mathbb{D}_1$,如第4节所述)上的预期差异(损失 $\mathcal{L}$):
$$ \theta^* = \arg\min_{\theta} \mathbb{E}_{(x,r)\sim\mathbb{D}_1} [\mathcal{L}(\mathcal{M}_\theta(x), r)] $$思维链推理 思维链(CoT)推理可以被形式化地定义为一个结构化的分解过程,将一个复杂的推理任务分解为一个显式的中间逻辑步骤序列。给定一个问题输入 $x$ 和一个目标输出 $y$,一个思维链推理过程 $\mathcal{R}$ 是一个包含 $K$ 个中间推理状态的序列 $\mathcal{R}(x) = (z_1, z_2, ..., z_K)$,其中每个 $z_i$ 代表一个原子的推理步骤,它将潜在状态从 $z_{i-1}$ 转换为 $z_i$,其中 $z_0$ 被隐式地定义为从 $x$ 派生的初始问题状态。每个推理步骤 $z_i$ 可以被描述为一个元组 $z_i = (s_i, j_i, u_i)$,其中 $s_i$ 代表符号状态(在步骤 $i$ 推导出的事实或断言的集合),$j_i$ 代表理由(应用的逻辑规则或推断),$u_i$ 代表不确定性估计(模型对这一推理步骤的置信度)。为简单起见,在上下文中明确的情况下,我们将使用符号状态 $s_i$ 来代表推理状态 $z_i$,因为它们在这项工作中有一对一的映射。我们在这项工作中也不使用 $u_i$ 估计,LLM被直接要求在每个CoT步骤中给出结果的符号状态。
表征有效思维链推理的两个重要属性是:(i)逻辑连贯性 [Wei et al., 2022b],和(ii)渐进式优化 [Du et al., 2025]。如果对于每个步骤 $z_i$(其中 $i > 1$),存在 $j_{i-1}$ 使得 $j_{i-1}(s_{i-1}) \Rightarrow s_i$,则CoT过程 $\mathcal{R}(x)$ 表现出逻辑连贯性,这意味着每个状态都是通过将一个合理的推理规则应用于前一个状态而逻辑地得出的。如果对于所有 $i \in \{1, 2, ..., K\}$,$I(z_i; y) > I(z_{i-1}; y)$,则CoT过程 $\mathcal{R}(x)$ 表现出渐进式优化,其中 $I(z_i; y)$ 代表推理状态 $z_i$ 和目标输出 $y$ 之间的互信息。
输入 在这项工作中,我们使用以下输入:(i)一个预训练的LLM $\mathcal{M}$,(ii)一个以PDDL表示的规划领域和问题的数据集 $\mathbb{D}$,及其解决方案(满足性规划),以及(iii)一个用于验证由 $\mathcal{M}$ 生成的规划正确性的规划验证器 $\mathcal{V}$。数据集 $\mathbb{D}$ 包括:
数据划分 如图1所示,我们的方法有三个阶段(更多细节见第5节)。为此,我们将数据集 $\mathbb{D}$ 划分为三个集合:$\mathbb{D}_1$、$\mathbb{D}_2$ 和 $\mathbb{D}_{test}$,分别用于第一阶段训练、第二阶段训练和评估。我们通过为每个问题添加不正确的规划来向 $\mathbb{D}_1$ 添加额外数据,类似于NaturalInstructions框架[Mishra et al., 2022, Wang et al., 2022]。
输出 主要输出是一个指令调优的模型 $\mathcal{M}_\theta$,具有增强的符号规划能力。该模型应展示出改进的领域表示、问题表示、规划生成、动作验证、规划验证和推理透明度。
假设 我们的框架假设规划领域遵循第3节中解释的特性,即不包含复杂的PDDL特性,例如条件效果或持续动作。这简化了推理链。
图1展示了我们通过逻辑思维链(CoT)指令调优来增强大型语言模型(LLMs)符号规划能力的综合框架。该方法包括两个训练阶段:初始指令调优和CoT指令调优。
[第一阶段] 初始指令调优阶段 在初始指令调优阶段(不同于简单的微调),我们采用一个预训练的LLM,并使用精心设计的提示对其进行训练,这些提示将规划领域和问题与它们解决方案的详细解释配对,所有这些都来自数据集 $\mathbb{D}_1$。如图1所示,我们不仅仅是让模型接触规划示例,而是明确地指示它通过解释前置条件的满足和效果的应用来分析规划中每个动作为何有效。
此阶段既包含正确的规划,也包含故意设置的错误规划,以教导模型识别和解释各种规划错误。对于不正确的规划,我们包括以下示例:(1)动作前置条件未满足,(2)效果应用不正确,(3)框架公理被违反,或(4)规划未能达到目标状态。通过让模型接触成功和失败的规划尝试及其详细解释,我们为逻辑验证奠定了基础。
此阶段建立了规划知识的基础,同时教导模型阐明动作有效性的逻辑理由,为后续阶段更高级的推理奠定了基础。本工作中使用的确切提示可在补充材料中找到。
[第二阶段] CoT指令调优阶段 我们方法的主要创新在于CoT指令调优阶段(在图1中用红色边界突出显示)。这第二阶段本身是一个两阶段的过程,将在下一节中详细描述。从高层次上看,在此阶段,初始调优的LLM使用强调完整逻辑推理链的结构化指令过程进行进一步训练。当呈现来自数据集 $\mathbb{D}_2$ 的领域和问题时,这个初始调优的模型会产生代表候选规划的逐步状态-动作-状态序列 $\langle s_0, a_1, s_1 \rangle, \langle s_1, a_2, s_2 \rangle, ..., \langle s_{n-1}, a_n, s_n \rangle$。
这些推理链随后通过一个使用 VAL [Howey et al., 2004] 实现的验证模块,该模块根据动作的前置条件和效果系统地检查每个状态转换的有效性。请注意,虽然一些方法尝试使用LLMs本身作为验证器,但研究表明,目前LLMs在推理方面不具备足够的自我纠正能力 [Huang et al., 2024, Stechly et al., 2025]。与模型试图在没有外部验证的情况下批判自己推理的自反思方法不同,我们的思维链方法明确地将规划过程分解为可验证的逻辑步骤,外部验证提供基准真相反馈。这种显式推理分解与验证反馈的结合,为增强规划能力创造了一个比仅仅依赖模型内部推理更可靠的基础。
我们探索了两种不同类型的验证反馈:(1)二进制反馈,仅指示动作是有效还是无效;(2)详细反馈,提供由VAL生成的关于每个动作的具体推理,说明哪些前置条件失败或哪些效果应用不正确。我们的假设是,详细反馈将通过提供关于推理过程中逻辑错误的明确指导,从而带来更强大的规划能力。
验证结果提供了关键的反馈,指导进一步的指令调优。这个反馈循环确保模型不仅学会生成语法正确的规划,还能推理其逻辑有效性。我们限制了这个反馈循环用于生成新CoT规划的次数,记为 $\eta$。$\eta$ 是一个我们可以变化以观察其如何影响准确性的超参数。
我们的PDDL-INSTRUCT方法通过其在每个规划步骤中对前置条件和效果的显式验证,优先考虑了逻辑连贯性(见第3节)。验证反馈确保每个状态转换都逻辑地遵循一个有效动作的应用,严格遵守领域规则。然而,我们的方法不保证渐进式优化(见第3节)。这是因为我们专注于生成能够实现目标的满足性规划,而不是优化最短或最高效的规划(这会在每一步增加与最优解的互信息)。在实践中,生成最优解是一个明显更困难的问题,无论对于经典规划器还是对于训练LLMs来生成它们都是如此 [Ray and Ginsberg, 2008, Domshlak and Nazarenko, 2013]。
我们PDDL-INSTRUCT框架的一个显著特点是在CoT指令调优中采用了两阶段优化过程,该过程明确地针对CoT的逻辑推理质量和最终的规划性能。这种方法通过确保模型不仅产生正确的规划,还通过逻辑思维链推理发展出强大的验证能力,来解决符号规划的独特挑战。该算法可在补充材料中找到。
第一阶段:推理链优化 在第一阶段,我们优化模型参数 $\theta_t$ 以提高高质量推理链的生成。具体来说,每个推理步骤 $r$ 中的模型权重 $\theta_t^r$(其中 $t \in [0, \eta-1]$)按公式2更新:
$$ \theta_t^r = \theta_t - \delta_1 \nabla_{\theta_t} \mathcal{L}_{reasoning}(\theta_t, \mathbb{D}_{reasoning}^t) \quad (2) $$其中 $\mathcal{L}_{reasoning}$ 是一个损失函数,用于衡量生成的推理链与理想逻辑推理序列相比的质量,$\delta_1$ 是此阶段的学习率,$\mathbb{D}_{reasoning}^t$ 是包含单个 $\langle s_{i-1}, a_i, s_i \rangle$ 三元组及其VAL反馈的数据集。这个目标鼓励模型产生能够正确(i)在应用动作前检查所有必要的前置条件;(ii)跟踪动作效果导致的状态变化;(iii)验证在整个规划过程中不变量得以维持;以及(iv)检测提议规划中的逻辑不一致性的分步推理。
推理损失明确惩罚逻辑错误,例如应用未满足前置条件的动作、未能正确传播效果或生成违反领域约束的步骤。通过专门关注推理过程,此阶段帮助模型发展出稳健规划所需的逻辑基础。
第二阶段:最终任务性能优化 在第二阶段,我们从经过推理改进的参数 $\theta_t^r$ 开始优化,以增强整体规划能力:
$$ \theta_{t+1} = \theta_t^r - \delta_2 \nabla_{\theta_t^r} \mathcal{L}_{final}(\theta_t^r, \mathbb{D}_{final}^t) \quad (3) $$其中 $\mathcal{L}_{final}$ 衡量最终输出与训练数据中预期答案的匹配程度,$\delta_2$ 是此阶段的学习率,$\mathbb{D}_{final}^t$ 包含领域、问题和从CoT输出中提取的规划,以及指定规划对该问题是否正确的VAL反馈。这第二阶段确保逻辑推理的改进能转化为产生准确规划的实际规划能力。
这种两阶段方法非常重要,因为第一阶段发展了规划所需的逻辑基础,而第二阶段确保这些能力被正确应用于生成正确的规划。这些目标的分离使我们的框架能够在教授基本推理技能和优化特定任务性能之间取得平衡,从而产生不仅能生成正确规划,还能通过显式逻辑CoT推断来推理其正确性的模型。损失函数 $\mathcal{L}_{reasoning}$ 和 $\mathcal{L}_{final}$ 的确切公式以及超参数的具体值在补充材料中有详细讨论。
在完成初始指令调优和CoT指令调优两个阶段后,最终模型将在评估阶段进行评估(如图1右侧所示)。在此阶段,指令调优的LLM将面对来自 $\mathbb{D}_{test}$ 的新的、未见过的规划领域和问题。模型直接生成完整的状态-动作-状态序列 $\langle s_0, a_1, s_1 \rangle, ..., \langle s_{n-1}, a_n, s_n \rangle$,构成其对规划问题的提议解决方案。然后使用VAL评估这些生成的规划的正确性,但仅用于评估目的,即不向模型返回反馈。只有当序列中的所有动作在其各自的状态下都适用,并且最终状态满足所有目标条件时,该规划才被认为是有效的。
我们对PDDL-INSTRUCT进行了全面的实验评估,以评估其在增强LLMs符号规划能力方面的有效性。我们的评估利用了PlanBench [Valmeekam et al., 2023b],这是一个用于评估LLM规划能力的标准化基准框架。
我们使用PlanBench评估PDDL-INSTRUCT,以评估其在增强LLMs符号规划能力方面的有效性。我们的实验旨在回答以下研究问题:
我们使用 Llama-3-8B 和 GPT-4² 基础模型实现了PDDL-INSTRUCT。我们将其与基线(未修改的模型)和第一阶段后的版本(在规划示例上进行指令调优,并附有每个规划有效或无效的推理)进行比较。对于PDDL-INSTRUCT,我们测试了带有二进制反馈(有效/无效)和详细反馈(由VAL生成的特定推理错误)的变体,每种变体的反馈迭代循环限制为 $\eta \in \{10, 15\}$。所有实验均在2个NVIDIA RTX 3080 GPU上进行。
领域和问题 PlanBench提供了一种系统化的方法,用于评估跨不同规划领域和问题复杂性的规划能力。我们在来自PlanBench的三个不同规划领域上进行评估,每个领域都提出了不同的推理挑战:
评估指标 我们的主要评估指标是规划准确率,衡量模型为多少比例的规划任务生成了达到指定目标的有效规划。一个规划只有在所有动作在其各自的状态下都适用,并且最终状态满足所有目标条件(由VAL验证)时,才被认为是有效的。对于每个领域,我们生成100个不同复杂度的测试任务,问题包括不同数量的对象并需要不同长度的规划来解决。
²注意GPT-4实验因访问受限而受到限制。
总体性能(RQ1) 表1展示了不同模型、领域和方法下的规划准确率。结果清楚地表明,PDDL-INSTRUCT显著优于基线模型、仅经过第一阶段指令调优的模型以及仅经过第二阶段CoT指令调优的模型。
对于Llama-3,使用详细反馈和 $\eta=15$ 的PDDL-INSTRUCT在Blocksworld、Mystery Blocksworld和Logistics领域中分别达到了94%、64%和79%的有效率。这代表着比基础指令调优平均绝对提升了35%(标准差=20%),比基线模型平均绝对提升了66%(标准差=3%)。同样,对于GPT-4,使用详细反馈和 $\eta=15$ 的PDDL-INSTRUCT在这三个领域中分别达到了91%、59%和78%的有效率。这代表着比基础指令调优平均绝对提升了48%(标准差=5%),比基线模型平均绝对提升了61%(标准差=9%)。这些结果表明,逻辑CoT指令调优显著提高了规划准确率,不仅与未修改的基础模型相比,更重要的是,与仅进行基础指令调优的模型相比也是如此。关于前置条件、效果和状态转换的显式推理使模型能够生成准确的规划。
| 模型 | 领域 | 基线 | 仅P1 | 仅P2(详细) | PDDL-INSTRUCT (二进制) | PDDL-INSTRUCT (详细) | ||
|---|---|---|---|---|---|---|---|---|
| $\eta=15$ | $\eta=10$ | $\eta=15$ | $\eta=10$ | $\eta=15$ | ||||
| Llama-3 | Blocksworld | 28% | 78% | 72% | 84% | 89% | 91% | 94% |
| Mystery BW | 1% | 32% | 17% | 47% | 49% | 59% | 64% | |
| Logistics | 11% | 23% | 45% | 61% | 72% | 75% | 79% | |
| GPT-4 | Blocksworld | 35% | 41% | 76% | 84% | 79% | 91% | 87% |
| Mystery BW | 3% | 17% | 19% | 44% | 39% | 59% | 54% | |
| Logistics | 6% | 27% | 51% | 69% | 64% | 72% | 78% | |
反馈类型的影响(RQ2) 比较表1中的二进制反馈和详细反馈列,我们观察到详细反馈在所有领域和模型中都始终优于二进制反馈。对于Llama-3($\eta=15$),与二进制反馈相比,详细反馈在Blocksworld、Mystery Blocksworld和Logistics领域中分别将规划准确率提高了5个、15个和7个百分点。值得注意的是,我们的训练方法虽然是独立开发的,但与LEPA [Zhang et al., 2025a]有相似之处,后者也表明提供关于每个动作失败原因的具体反馈有助于提高LLMs的推理能力。
这一模式证实了我们的假设,即提供具体的推理错误有助于模型发展出更强大的验证能力。详细反馈的优势在Mystery Blocksworld这个谓词被混淆的最复杂领域中尤为明显。此外,我们观察到将迭代限制从 $\eta=10$ 增加到 $\eta=15$ 在所有配置中都带来了持续的改进。这一观察表明,模型在给予额外的反馈迭代循环后可能会收敛到有效的规划,尽管需要未来的实验来改变η以证实这一点。这种改进在使用详细反馈时更为显著(在所有领域和模型中平均提高4.3个百分点),而不是二进制反馈(平均提高3.3个百分点),这表明详细反馈能够更有效地利用额外的推理迭代。
跨领域泛化(RQ3) 我们的结果显示了不同领域之间性能的显著差异,反映了它们固有的复杂性和推理挑战。两个模型在Blocksworld上表现最好,其次是Logistics,而Mystery Blocksworld被证明是最具挑战性的。对于Llama-3(详细反馈,$\eta=15$),Blocksworld的有效率为94%,Logistics为79%,Mystery Blocksworld为64%。这种模式在所有配置和模型中都是一致的,突显了具有隐藏谓词和复杂状态交互的领域难度不断增加。值得注意的是,虽然绝对性能在不同领域有所不同,但PDDL-INSTRUCT带来的相对改进在这三个领域中都是显著的。这表明我们的方法以一种领域通用的方式增强了规划能力,逻辑推理框架在不同的规划场景中都得到了有效的迁移。
最大的相对改进发生在基线性能最弱的领域。例如,Llama-3在Mystery Blocksworld上的性能从仅1%提高到64%(使用PDDL-INSTRUCT,详细反馈,$\eta=15$),代表了64倍的提升。在最具挑战性的领域中取得如此显著的增强,表明显式逻辑推理对于简单模式匹配不足以解决的复杂规划场景尤其有价值。
我们提出了PDDL-INSTRUCT,一个通过逻辑思维链指令调优显著增强大型语言模型符号规划能力的新颖框架。通过将规划过程分解为可验证的逻辑推理链并提供明确的验证反馈,我们的方法使LLMs能够在不同规划领域中生成具有前所未有可靠性的有效规划。虽然我们的结果很有前景,但我们注意到我们的方法并未在所有领域达到100%的准确率。然而,当与像LLM-Modulo [Kambhampati et al., 2024] 这样的框架结合时——该框架为LLMs与外部工具的集成提供了高效机制——我们的方法可以显著减少与验证器所需的反馈循环次数。这种集成将通过允许模型利用其增强的推理能力,同时在需要时仍然受益于形式验证,从而使规划过程更加高效,最终实现更快、更可靠的规划。
我们基于VAL的验证方法的一个显著优势是其对Lyu等人[2023]描述的不忠实思维链推理的鲁棒性。虽然传统的CoT方法可能生成听起来合理但内部不一致的推理链,我们的外部验证确保每个逻辑步骤都根据规划领域的约束进行了形式化验证。
局限性与未来工作 尽管我们的结果突显了将逻辑思维链与验证引导的反馈相结合的有效性,但未来仍有几个有前景的方向: