摘要 (Abstract)
以自注意力机制为核心的Transformer网络,是大型语言模型(LLM)的基石。在生成式任务中,模型会缓存(cache)已生成词元(token)的键(Key)和值(Value)投影,以避免重复计算。然而,在传统的图形处理器(GPU)架构中,每生成一个新词元,都必须将巨大的KV缓存从高带宽内存加载到片上静态随机存取存储器(SRAM)中,这造成了严重的延迟和能耗瓶颈。为此,我们提出了一种定制的自注意力内存计算(in-memory computing, IMC)架构。该架构基于一种名为“增益单元”(gain cell)的新兴电荷存储器件,它能高效地写入新词元的KV值,并直接在存储阵列内并行执行注意力机制所需的模拟点积运算。然而,模拟电路固有的非理想性和硬件约束,使得直接部署预训练模型变得不可行。为解决这一难题,我们设计了一种专门的初始化算法,使我们的硬件模型无需从零开始训练,即可达到与GPT-2相当的文本处理性能。与GPU相比,我们的架构将注意力计算的延迟和能耗分别降低了高达两个和四个数量级,这标志着我们朝着实现超快速、低功耗的生成式Transformer迈出了坚实的一步。
引言:挣脱“内存墙”的束缚
大家好,我是这项研究的主要贡献者之一。今天,我想和大家分享我们是如何从一个看似疯狂的想法出发,最终设计出一套可能改变大型语言模型(LLM)未来的硬件架构。我们每天都在惊叹于LLM的强大能力,但其背后是惊人的计算资源消耗。每一次与AI的对话,每一次代码生成,都伴随着数据中心里GPU风扇的呼啸。这其中最大的“电老虎”之一,就是Transformer模型的心脏——注意力机制。
想象一下,当模型逐字生成一篇文章时,它需要不断“回顾”前面已经写下的所有内容,以确保上下文连贯。这个“回顾”的过程,就是通过注意力机制完成的。模型会将每个新生成的词(Query)与所有历史词(Key)进行匹配度计算,然后根据匹配度(Attention Score)加权“提取”历史词的信息(Value)。为了效率,所有历史词的Key和Value都会被存储在一个叫“KV缓存”的地方。
问题来了:在GPU上,这个KV缓存通常存放在速度较慢但容量大的主内存(HBM)里。每生成一个新词,整个庞大的KV缓存就要被搬运到GPU核心旁边的高速缓存(SRAM)中进行计算。这个过程就像一个图书馆管理员,为了找一本书(计算当前词),需要先把整个图书馆的书(KV缓存)都从仓库搬到阅览室。这种数据搬运的成本,就是所谓的“内存墙”,它极大地限制了LLM的生成速度,并消耗了巨量能源。我们不禁要问:有没有办法让数据在存储的地方直接进行计算,从而彻底拆掉这堵墙?
核心构想:会计算的存储单元——增益单元(Gain Cell)
我们的答案是肯定的,而实现这一构想的关键,是一种名为增益单元(Gain Cell)的特殊存储器件。你可以把它想象成一个“聪明”的微型水杯。
- 存储 (Writing):我们通过一个“水龙头”(写晶体管)向这个水杯里注入一定量的“水”(电荷),水面的高度(电容上的电压 \(V_{store}\))就代表了我们要存储的数值,比如一个Key或Value。
- 计算 (Reading/Computing):这个水杯旁连接着一个“水泵”(读晶体管)。水泵的抽水速度(输出电流 \(I_{cell}\))会根据杯中水位的高低自动调节。水位越高,抽水越快。
最奇妙的是,我们可以让一个外部信号——比如代表Query的脉冲信号——来控制这个“水泵”的开关。当Query脉冲到来时,水泵开启,产生一股与“存储值(水位)”和“输入Query(开关时长)”都相关的“水流”(电流)。这就是一次乘法运算!当我们把成千上万个这样的“水杯-水泵”系统(增益单元阵列)并联起来,它们的“水流”在同一根“管道”(位线 Bitline)上汇集,根据基尔霍夫电流定律,总水流量就是所有单个水流之和。这不就天然地完成了乘加(Multiply-Accumulate, MAC)运算,也就是点积的核心吗?
通过这种方式,数据(Key和Value)被存储在增益单元的电容里,而计算(与Query的点积)则在原地瞬间完成,几乎没有数据搬运。这就是模拟内存计算(Analog In-memory Computing)的魅力所在。
交互动画1:增益单元的工作原理
这个动画模拟了一个简化的增益单元。你可以通过滑块调整存储在电容上的电压(相当于Key/Value值),然后点击“施加Query脉冲”按钮,观察输出电流如何根据存储电压和输入脉冲而变化。这直观地展示了乘法是如何在模拟域实现的。
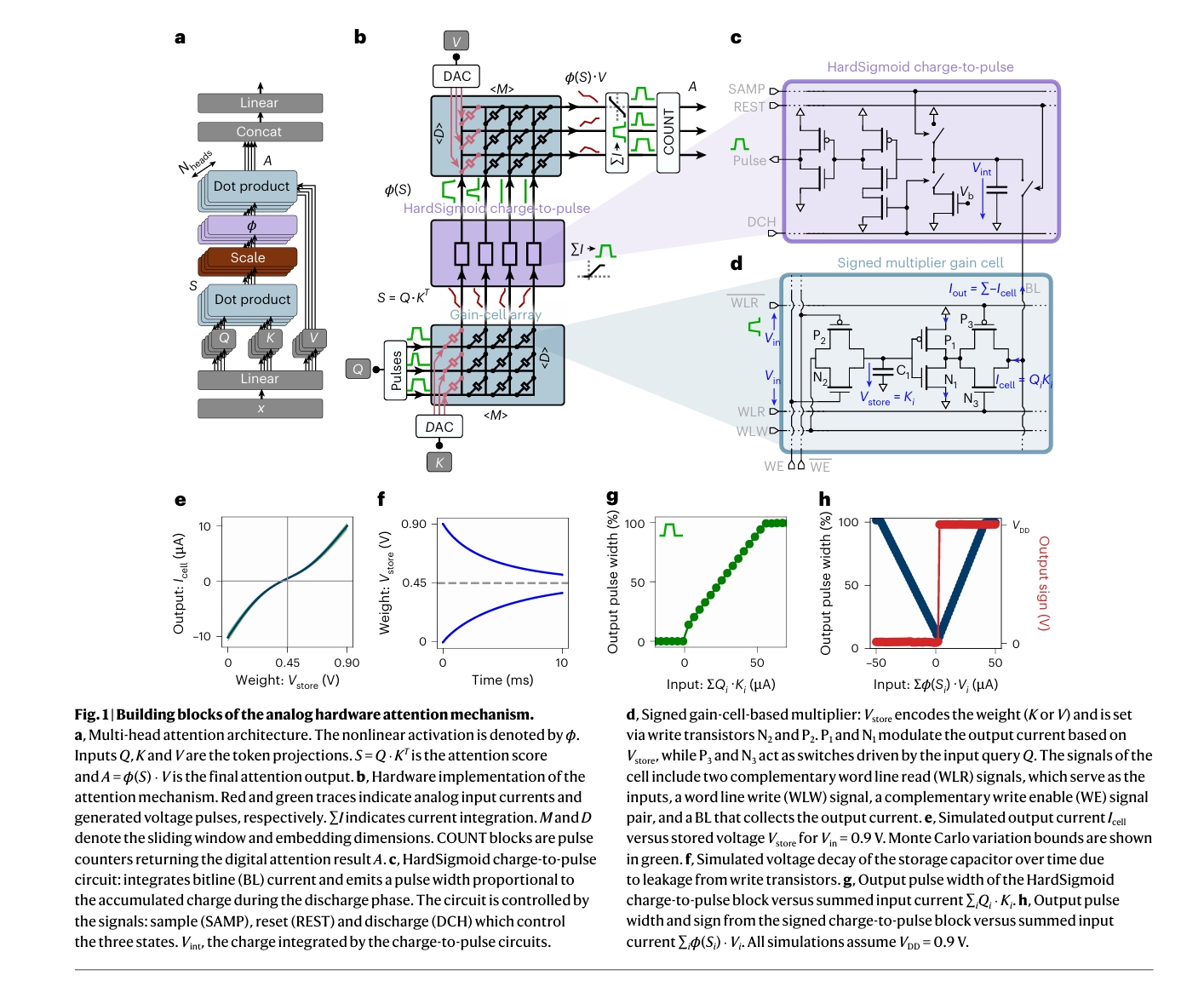
端到端的模拟计算流程:从电荷到脉冲的舞蹈
仅仅完成点积还不够。一个完整的注意力计算流程是 \(A = \phi(Q \cdot K^T) \cdot V\),其中 \(\phi\) 是一个非线性激活函数,通常是Softmax。要在我们的模拟硬件中复现这个流程,我们设计了一套精巧的“电路接力赛”。
第一棒:Q·KT 点积。 如图(b)所示,我们用两个增益单元阵列分别存储K和V。输入的Query被编码成一系列宽度可变的电压脉冲(脉宽调制,PWM)。这些脉冲被施加到K阵列的行上,驱动每个增益单元进行乘法运算。同一列上所有单元的输出电流在位线上汇合,完成点积,得到注意力得分 \(S = Q \cdot K^T\)。
第二棒:非线性激活 \(\phi\)。 Softmax函数计算复杂,因为它需要对所有得分求和并进行归一化,这在模拟硬件中难以实现。我们另辟蹊径,采用了一个更“硬件友好”的函数——HardSigmoid。我们设计了一个“充放电-脉冲转换”电路(Charge-to-Pulse Circuit),如图(c)所示。它就像一个计时沙漏:
- 积分(充电):来自K阵列的输出电流(代表 \(S\))会给这个电路里的一个小电容充电。电流越大,充电越快,电容上积累的电荷就越多。
- 转换(放电并计时):在一个固定的放电阶段,我们测量这个电容完全放电需要多长时间。积累的电荷越多,放电时间就越长。我们将这个放电时间作为输出脉冲的宽度。
这个过程巧妙地实现了 \( \phi(S) \)。当输入电流(\(S\))很小时,输出脉冲很窄;随着电流增大,脉冲宽度线性增加;当电流大到一定程度,电容被充满,脉冲宽度达到最大值并饱和。这恰好模拟了HardSigmoid函数的行为:抑制、线性、饱和。
交互动画2:电荷-脉冲转换 (HardSigmoid)
演示HardSigmoid激活函数的硬件实现。拖动滑块模拟来自Q·KT点积的输入电流。观察电路如何将电流积分(充电),然后生成一个宽度与积分电荷成正比的输出脉冲。注意观察当输入电流过大时,输出脉冲宽度会饱和。
输出脉冲宽度: 50.0%
第三棒:\(\phi(S) \cdot V\) 点积。 HardSigmoid电路输出的脉冲(代表 \(\phi(S)\))被作为新的输入,施加到存储着V的第二个增益单元阵列上。同样地,通过模拟内存计算,我们得到了最终的注意力输出 \(A = \phi(S) \cdot V\)。
终点冲刺:数字化。 最后的输出电流经过一个带符号的充放电电路,生成最终的脉冲和符号位,再由一个数字计数器(Counter)精确测量脉冲宽度,将其转换为数字信号。至此,一次完整的注意力计算在模拟域高效完成后,结果被干净利落地交还给数字世界。
高级动画3:信息流场
这个动画并非直接模拟电路,而是通过柏林噪声驱动的粒子流场,艺术化地展现了模拟计算中信息流动的复杂与和谐。成千上万的粒子在看不见的力量场中优雅地运动,形成涡流和轨迹,象征着模拟信号在增益单元阵列中并行、动态地交互与整合。这体现了我们架构的内在美学:用简洁的物理定律,实现高效而强大的计算。
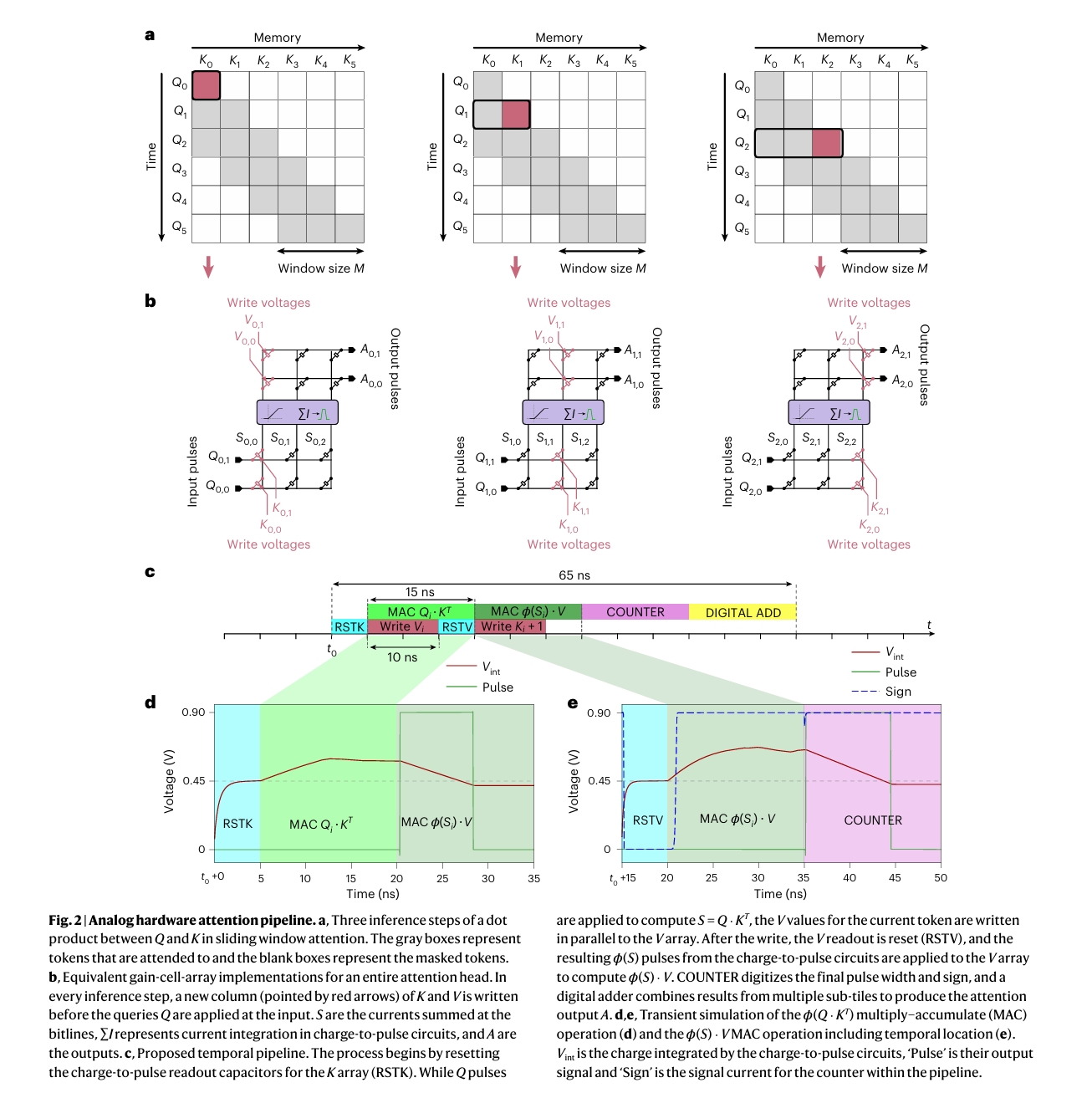
时序之舞:滑窗注意力与流水线操作
为了处理长序列并控制硬件规模,我们采用了滑窗注意力(Sliding Window Attention)机制。这意味着,在计算当前词的注意力时,我们只“回顾”最近的M个历史词,而不是全部历史。这就像一个人的短期记忆,容量有限但更新迅速。
在硬件上,这意味着我们的K和V增益单元阵列只需要M列。每生成一个新词,我们会将它的K和V值写入阵列的下一列。当所有M列都写满后,就回到第一列进行覆盖。这个过程就像一个循环队列,不断丢弃最旧的记忆,接纳最新的信息。
交互动画4:滑窗注意力数据流
本动画展示了滑窗注意力机制的动态过程。每点击一次“生成新词元”,一个新的(K, V)对就会被写入数组的下一列(高亮显示),而注意力计算窗口(灰色区域)也随之向右滑动。当窗口到达末端后,写操作会回到第一列,实现循环覆盖。这模拟了模型在生成文本时,KV缓存的实时更新过程。
当前时间步: 0 | 写入位置: 0
更进一步,为了极致的效率,我们设计了精密的流水线(Pipeline)操作时序,如论文图2c所示。当K阵列正在进行 \(Q \cdot K^T\) 计算时,我们并不会让V阵列闲着,而是同步地将当前词的V值写入V阵列。这样,计算和写入操作无缝衔接,大大缩短了每个时间步的处理延迟。整个过程就像一条高效的工厂流水线,每个部件都在争分夺秒地工作,最终将单次注意力计算的延迟压缩到了惊人的65纳秒。
静态图1:计算流水线时序
这张图详细分解了65纳秒内完成一次注意力计算的流水线操作。它清晰地展示了K阵列复位(RSTK)、Q·KT乘加(MAC)、V值写入、V阵列复位(RSTV)、Φ(S)·V乘加以及最终计数器(COUNTER)等步骤是如何在时间上精密交错、并行执行的。
bridging the Gap: 从软件到硬件的“翻译”艺术
我们面临的最大挑战是:模拟电路的行为并非理想的线性数学运算,它存在非线性、噪声和器件差异。同时,我们的架构使用了HardSigmoid而非Softmax,还引入了滑窗和量化。这些“硬件方言”与预训练的GPT-2模型所使用的“标准语言”格格不入。直接将GPT-2的权重搬到我们的芯片上,结果必然是胡言乱语。
从零开始训练一个适配硬件的模型成本太高。于是,我们开创了一套巧妙的硬件感知映射与微调(Hardware-aware Mapping and Fine-tuning)流程,它就像一个高明的翻译官。
- 构建中间模型 (Linear Hardware Model): 我们先创建一个“中间语言”模型。这个模型在软件中模拟了除了增益单元非线性之外的所有硬件特性,如滑窗、HardSigmoid激活和量化。然后,我们将预训练的GPT-2权重迁移过来,并进行短暂的微调(fine-tuning)。这就像让翻译官先学习硬件的“语法规则”。实验证明(图4d蓝线),这个模型能很快达到与原版GPT-2相近的性能。
- 非线性适应算法: 接下来是最关键的一步:处理增益单元的非线性“口音”。我们发现,这种非线性会扭曲数据流的统计分布(均值和方差)。为此,我们设计了一个迭代适应算法。我们在模型的关键节点插入了可学习的缩放(\(y=ax+b\))层。算法会迭代调整这些a和b参数,直到非线性模型中数据流的统计分布与我们之前训练好的线性中间模型完全匹配。这就像翻译官在不断调整用词,以确保翻译后的句子不仅意思对,连“语气”和“强调”都和原文一模一样。如图4c所示,这个过程能迅速将模型的困惑度(Perplexity)从灾难性的高位拉回到一个非常合理的水平。
- 最后冲刺微调: 经过适应算法的“校准”后,我们再对整个非线性硬件模型进行最后的微调,进一步弥补性能差距。
交互动画5:非线性适应算法的可视化
此动画演示了适应算法的核心思想。左侧是理想线性模型的数据分布,右侧是带有非线性效应的硬件模型。通过调整缩放因子'a'和偏置'b',观察右侧的分布如何逐渐逼近左侧的目标分布。这揭示了我们如何通过简单的线性变换来补偿复杂的非线性失真。
分布匹配度: ...
最终结果令人振奋:通过这套流程,我们的模拟硬件模型在多项自然语言处理基准测试中,取得了与软件实现的GPT-2模型相当甚至更好的成绩。我们成功地在截然不同的硬件范式上,复现了先进LLM的能力。
成果与展望:数量级的飞跃
通过详尽的电路仿真和系统级评估,我们的架构展现了惊人的性能优势。与Nvidia H100这样的顶级数据中心GPU相比,在注意力计算这个环节上,我们的设计:
- 延迟降低了约100倍(65纳秒 vs. 微秒级)。
- 能耗降低了约70,000倍(6.1纳焦/词元 vs. 数百微焦/词元)。
这是一个革命性的提升。它意味着未来的LLM推理可能不再是大型数据中心的专属,而是可以被集成到边缘设备、移动终端,甚至个人电脑中,实现即时、高效、低功耗的智能交互。
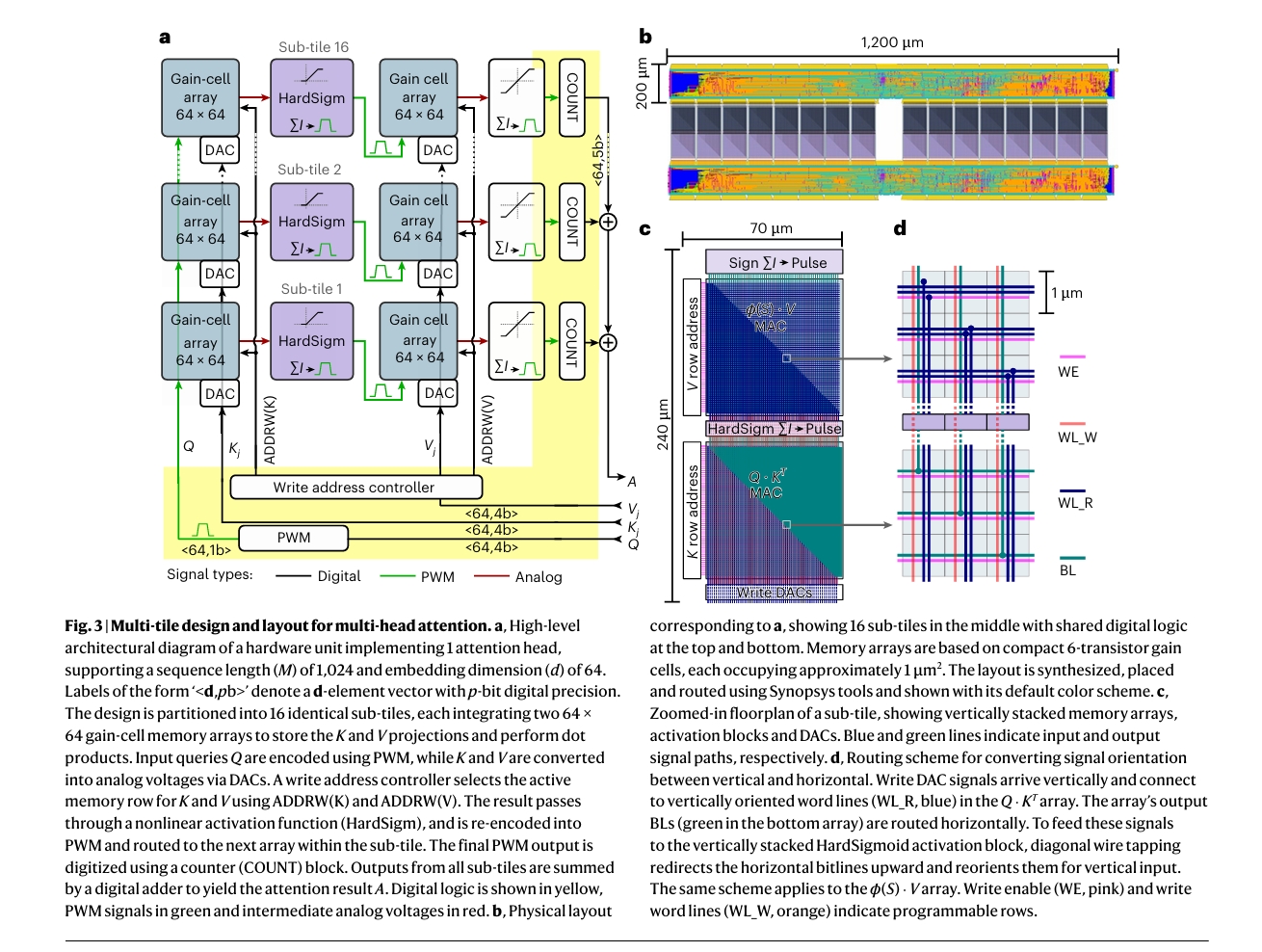
静态图2:多头注意力硬件架构
这张图展示了如何将我们设计的基础模块扩展为支持GPT-2所需的多头、大维度注意力机制。通过将多个64x64的子阵列(Sub-tile)并行排列,我们可以构建出支持1024窗口长度和多注意力头的完整计算单元。最终来自所有子阵列的结果通过数字加法器汇总,得到最终输出。
当然,这只是万里长征的第一步。我们目前的工作聚焦于注意力机制这一核心瓶颈。一个完整的LLM加速器还需要高效的线性层(Feed-Forward Networks)实现方案。幸运的是,内存计算同样适用于线性层。未来,我们将致力于将我们的注意力模块与其他内存计算技术集成,打造一个完整的、超低功耗的LLM片上系统。
此外,基于氧化物半导体(如IGZO)的增益单元技术,有望实现更低的功耗、更长的电荷保持时间,以及真正的三维堆叠,从而在更小的芯片面积上集成更强大的计算能力。我们相信,通过硬件与算法的协同优化,模拟内存计算将为通用人工智能的普及和可持续发展,开辟一条全新的道路。
附录:技术细节与公式解析
1. 签名的增益单元乘法器
论文图1d展示了我们设计的“签名增益单元”。它实际上由两个互补的增益单元构成,能够处理正负数。存储的权重 \(K_i\) 或 \(V_i\) 被编码为差分电压 \(V_{store}\) 存储在电容 \(C_1\) 上。当输入查询Q的脉冲信号(通过WLR和WLRD)到来时,P1/N1晶体管对会根据 \(V_{store}\) 的值产生一个推(push)或拉(pull)的电流。最终输出的总电流 \(I_{out} = \sum I_{cell}\) 正比于输入脉冲宽度和存储电压的乘积。图1e中的仿真曲线展示了输出电流 \(I_{cell}\) 与存储电压 \(V_{store}\) 之间的非线性关系,这正是我们需要在软件模型中精确建模和补偿的关键。
在我们的硬件感知模型中,这个非线性点积被建模为三阶多项式,以在训练中准确反映硬件行为: \[ S = \sum_{n=1}^{N_{tokens}} \sum_{i=0}^{3}\sum_{j=0}^{3-i} Q_n \cdot (K_n - K_{offset})^{i} V_{in}^{j} C_{i,j} \] 其中 \(Q_n\) 是输入脉冲宽度,\(K_n\) 是存储的电压,\(K_{offset}\) 是中心电压(0.45V),\(V_{in}\) 是固定的读取电压,\(C_{i,j}\) 是从SPICE仿真中拟合出的多项式系数。
2. HardSigmoid 充放电电路
图1c是HardSigmoid电路的简化原理图。其行为可以用以下分段函数来精确描述: \[ \phi(S) = \begin{cases} W_{max} & \text{if } S \ge S_{sat} \\ \frac{W_{max}}{S_{sat}}S & \text{if } 0 < S < S_{sat} \\ 0 & \text{if } S \le 0 \end{cases} \] 其中 \(S\) 是积分后的输入电流总和, \(S_{sat}\) 是电路饱和的电流阈值, \(W_{max}\) 是最大输出脉冲宽度(在我们的设计中是15ns)。这个函数在软件中实现起来非常简单,并且梯度清晰,有利于反向传播训练。
3. 电荷泄漏与时间衰减
增益单元的电容存储不是永久的,电荷会随着时间慢慢泄漏(如图1f)。这意味着存储的K和V值会随时间衰减。在我们的仿真中,我们将这种指数衰减建模为一个衰减掩码 \(\alpha\)。有趣的是,这种“遗忘”机制不完全是坏事。它类似于一些先进Transformer模型中有意引入的“线性偏置注意力”(如AliBi),可以帮助模型更好地处理长距离依赖关系。在我们的实验中,我们选择了一个非常保守的衰减率,并证明其对模型性能影响甚微。
静态图3:软件到硬件映射流程
此图总结了我们从预训练的软件模型(左)到最终的非线性硬件模型(右)的完整映射和训练流程。它清晰地展示了中间线性硬件模型的角色,以及适应算法是如何作为桥梁,将理想模型的权重“翻译”为能够适应硬件非线性的权重。