量子微分同胚无法使不确定因果序变得确定

引言：时空的迷雾与因果的罗盘

大家好，我是本文的作者之一。今天，我想邀请大家与我一同踏上一段奇妙的旅程，去探索物理学中最令人着迷的边界之一：时间的流动与因果的奥秘。在我们的日常经验中，因果关系如同一条笔直的单行道。我按下开关，灯亮了；我松开苹果，它落地了。“原因”总是在“结果”之前，从未有过例外。这似乎是宇宙中最不容置疑的铁律。

然而，当我们深入到量子力学那光怪陆离的微观世界，这条清晰的因果之链开始变得模糊，甚至出现了“分岔”。想象一下，如果一个事件A既可以在事件B之前发生，也可以在事件B之后发生，而且这两种可能性同时真实存在，构成一种“叠加态”。这就是我们所说的不确定因果序（Indefinite Causal Order, ICO）。这听起来像是科幻小说，但它却是量子理论所预言的一种真实可能性。

这场探索的起点，源于一个长期困扰物理学界的争论。我们已经通过“量子开关”（Quantum Switch）在实验室里实现了不确定因果序，但这究竟是真正操纵了时空的因果结构，还仅仅是一场精妙的“模拟”？

一些人认为，只有当引力场本身——也就是时空本身——处于叠加态时（我们称之为“引力量子开关”），才算是“真正的”不确定因果序。而目前实验室中用光子路径叠加实现的“光学量子开关”，则被看作是一种模拟。我们的研究，正是为了拨开这层迷雾，为这场争论提供一个清晰的答案。我们将借助广义相对论的语言，提出一个统一的框架，证明这两种“开关”在本质上是等价的。

第一章：重新定义“先后”——固有时间的裁决

要理解不确定因果序，我们首先要精确地定义“什么是因果序”。在量子信息领域，我们通常从“能否发送信号”来判断。如果A能影响B，那么A就在B之前。但在广义相对论的弯曲时空中，这个概念需要更坚实的基础。我们提出的核心思想非常直观：用固有时间（Proper Time）来做裁决。

想象一个勇敢的粒子（我们的“信使”）在时空中旅行，它的世界线是 \(\gamma_0\)。旅途中，它会先后与两个系统A和B相互作用（比如进入两个实验室）。这两个相互作用，我们称之为事件 \(\mathcal{E}_A\) 和 \(\mathcal{E}_B\)。信使手腕上戴着一块完美的“手表”，记录着它自身流逝的时间，这就是固有时间 \(\tau\)。那么，信使在遇到A和B时，它的手表分别读作 \(\tau_A\) 和 \(\tau_B\)。

我们的定义很简单：因果序就是固有时间差 \(\Delta\tau = \tau_B - \tau_A\) 的符号 \(s = \text{sign}(\Delta\tau)\)。如果 \(s = +1\)，意味着B发生在A之后；如果 \(s = -1\)，则A发生在B之后。这个定义的美妙之处在于，固有时间是一个“洛伦兹不变量”，无论你选择什么样的坐标系去观察，这个时间差的符号是不会改变的。它是由时空几何本身决定的，其计算公式为： \[ \tau_{\gamma} = \frac{1}{c} \int_{p_{\gamma,i}}^{p_{\gamma,f}} \sqrt{-g_{\mu\nu}dx^{\mu}dx^{\nu}} \] 其中 \(g_{\mu\nu}\) 是描述时空弯曲的度规张量。

第二章：量子开关——两种风味的“因果叠加”

有了对因果序的精确定义，我们来看看实现ICO的“量子开关”。它就像一个量子版的铁路岔道。一个目标粒子（比如一个光子）同时走向两条路径，一条是先经过A实验室再到B实验室，另一条是先B后A。由于路径处于叠加态，最终粒子经历的就是两种因果序的叠加。其状态可以写成： \[ |\Psi\rangle = \frac{1}{\sqrt{2}} \left( |0\rangle_C U_B U_A |\psi\rangle_T + |1\rangle_C U_A U_B |\psi\rangle_T \right) \] 这里，\(|0\rangle_C\) 和 \(|1\rangle_C\) 是控制系统（岔道开关）的状态，\(|\psi\rangle_T\) 是目标粒子的初始状态，\(U_A, U_B\) 是两个实验室进行的操作。

光学量子开关：路径的叠加

这是目前已在实验室中实现的版本。我们让一个光子同时通过两条空间上分离的光纤路径。一条路径上，光纤先连接到设备A，再到设备B；另一条则相反。时空背景是固定的（比如实验室里的普通时空）。在这里，因果序的不确定性，源于粒子“在哪里”的不确定性。在我们的定义下，这意味着在叠加的两个分支里，事件发生的坐标点 \(p_{\mathcal{E}_A}, p_{\mathcal{E}_B}\) 是不同的，从而导致了不同的固有时间顺序。

动画2：光学量子开关 (路径叠加)

一个粒子（光球）同时沿两条路径前进。一条路径先穿过紫色方块(A)，再穿过粉色方块(B)。另一条路径顺序相反。最终它们在出口干涉，携带了两种顺序的“记忆”。

▶️ 开始 🔄 重置

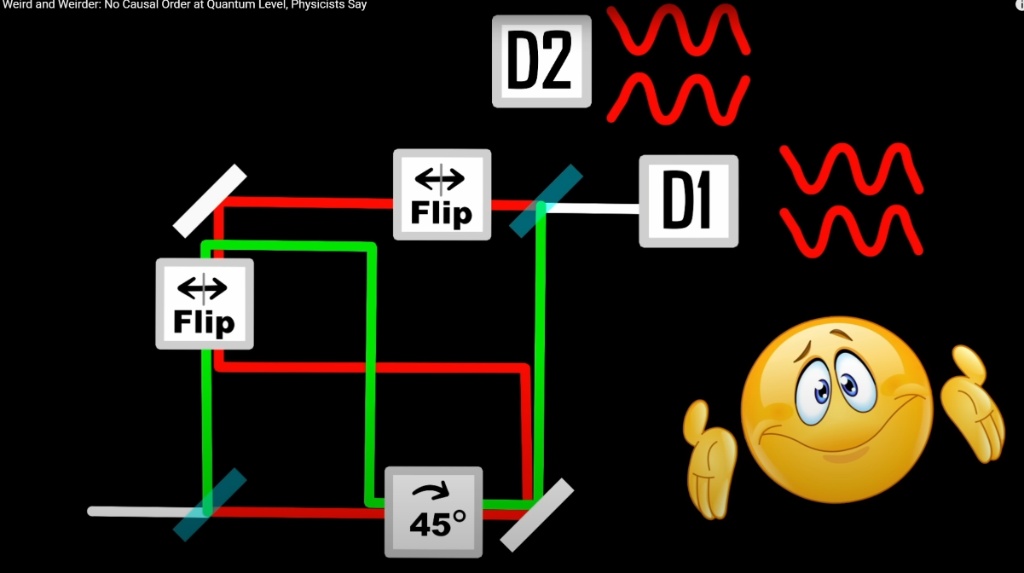
状态: 待开始

引力量子开关：时空的叠加

这是一个思想实验，被认为是更“根本”的ICO。想象一个巨大质量的物体（比如一颗小行星）被置于两个位置的叠加态。根据广义相对论，质量会使周围的时空弯曲。因此，这个叠加的质量会创造出一个叠加的引力场，也就是时空度规 \(g_{\mu\nu}\) 的叠加。现在，我们的信使粒子沿着一条固定的路径飞过这个区域。在质量位于位置1的分支中，时空是一种弯曲方式，信使经历的时间流逝速率是一种；在质量位于位置2的分支中，时空是另一种弯曲方式，时间流逝速率也不同。这种时间膨胀效应的差异，即使路径完全相同，也可能导致信使与A、B相遇的先后顺序发生反转。

第三章：终极对称性——量子微分同胚

现在，我们来到了我们研究的核心。表面上看，光学开关是“路径叠加”，引力开关是“时空叠加”，它们似乎截然不同。但我们发现，这种区分其实是人为的，它取决于你如何选择“坐标系”。在量子世界里，坐标系本身也可以是量子化的。我们引入了一个强大的概念——量子微分同胚（Quantum Diffeomorphism）。

在经典广义相对论中，“微分同胚”意味着物理定律不应依赖于你如何标记时空中的点（即坐标选择的自由）。量子微分同胚则是这个思想的量子升级版：它允许我们在一个量子叠加的每一个分支里，独立地、任意地选择不同的坐标系。

这就像什么呢？想象一下，你在分析一部电影的两个平行宇宙结局。量子微分同胚就像一个神奇的剪辑工具，允许你对一个结局的画面进行任意的拉伸、扭曲（改变坐标），同时对另一个结局的画面做另一套完全不同的拉伸、扭曲。

关键的发现是：我们定义的因果序指标，也就是两个分支中固有时间差符号的乘积 \(s^{(1)}s^{(2)}\)，在这个强大的“量子剪辑”操作下，是完全不变的！如果开始时是ICO（\(s^{(1)}s^{(2)}=-1\)），那么无论你怎么变换坐标，它始终是ICO。因果序的确定性或不确定性，是一个深刻的、内禀的物理属性，不随你的描述方式而改变。

第四章：视角的游戏——从“路径不同”到“时空不同”

量子微分同胚的不变性带来了一个惊人的推论：“路径叠加”和“时空叠加”只是描述同一种物理现实的两种不同语言。 我们可以通过一个巧妙的坐标变换，将一个光学量子开关“变”成一个看起来像引力量子开关的样子，反之亦然。

想象我们从一个光学开关开始：时空是平直的（度规\(g_{\mu\nu}\)是确定的），但粒子的两条世界线在时空中的位置不同。现在，我施展“量子微分同胚”的魔法，在两个分支中选择两套不同的坐标变换，精心设计它们，使得变换之后，两条原本不同的世界线被“拉直”并重合在了一起。这样一来，事件发生的“地点”就变得确定了。但是，代价是什么呢？代价是，为了强行对齐路径，我不得不扭曲了坐标网格，这导致原本平直单一的度规 \(g_{\mu\nu}\) 在两个分支中变成了不同的、弯曲的形式。瞧，一个“路径叠加”的ICO，就这样被我重新描述成了一个“时空叠加”的ICO。

这个过程是完全可逆的。这雄辩地证明了，纠结于ICO的根源是路径还是时空，就像争论一个物体是“在动”还是“静止”一样——答案取决于你选择的参考系。

结论：光学开关是“真”的，未来已来

我们的旅程即将到达终点。通过引入基于固有时间的因果序定义，并揭示其在量子微分同胚下的不变性，我们最终得出结论：

光学量子开关并非模拟，它与引力量子开关一样，都是对不确定因果序的真实物理实现。

将ICO的来源归咎于“路径”还是“时空”的叠加，是一种依赖于坐标选择的、人为的区分。这并不意味着我们否定了引力在时空结构中的核心作用，而是阐明了，要体验到量子因果的奇特效应，我们并不一定需要创造出宏观物体或时空的叠加。量子力学自身的结构，已经为我们提供了通往这片未知领域的钥匙。

这一结论意义重大。它为在现有技术框架内，利用光学等系统，深入研究和利用不确定因果序的计算优势铺平了道路，也为未来量子引力理论的探索提供了新的、更易于企及的实验和理论视角。时空的奥秘，或许比我们想象的更加触手可及。